
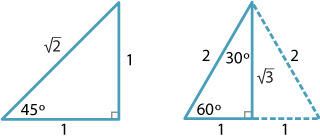
Viewing our trigonometric ratios as fractions, this is the same as Since corresponding sides of $\triangle ABC$ and $\triangle DEF$ are proportional, this means thatĬoncretely, $|DE| = \frac\right)^2 = 1. The last part of this task is ideally suited for group discussion where students can engage in MP3, Construct Viable Arguments and Critique the Reasoning of Others.īelow is a picture of a triangle $DEF$ whose angles are congruent to the corresponding angles of $\triangle ABC$ and whose sides are proportional (with scale factor 1/2) to the corresponding sides of $\triangle ABC$: It is good for students to see this right away, however, since it follows from the definitions of sine and cosine and the Pythagorean Theorem and this relationship is one of the main motivating factors for how the sine and cosine are defined. The teacher may need to provide guidance with part (d) if students have not yet seen the relationship (F-TF.8) $\cos^2(\angle A) + \sin^2(\angle A) = 1$. Parts (c) and (d) then address special properties of right triangles which make them ideally suited for these ratios. Here too, ratios of side lengths are equivalent for similar triangles. Example 2 For each triangle, find the unknown side lengths and trigonometric ratios for the angles. Leave your answers as radicals in simplest form. Explain 2 Trigonometric Ratios of Special Right Triangles You can use the relationships you found in special right triangles to find trigonometric ratios for the angles 45, 30, and 60. Special Right Triangles Date Period Find the missing side lengths. The task first investigates ratios of side lengths in a more general setting where the triangles in question are not necessarily right triangles. Find the unknown side lengths in each right triangle. These equivalent ratios provide the definition of the sine and cosine of any acute angle. Notice that 5:12:13 satisfies the Pythagorean theorem and is a common. In the special case when the triangles in question are right triangles and the ratio is that of a leg to the hypotenuse, these ratios depend, up to equivalence, only on the (acute) angle measures of the triangle. A 5-12-13 triangle is a right-angled triangle whose lengths are in the ratio of 5:12:13. You need to know the length of one side only to find the remaining sides. In such triangles, sides are proportional. They are special because, with simple geometry, we can know the ratios of their sides. Section 4.1 Special Right Triangles and Trigonometric Ratios 2 Two special°triangles are 3060° ☉0 °triangles and 45☄5 90°triangles. When two triangles are similar triangles ratios of their corresponding side lengths are equivalent. The other is the isosceles right triangle.
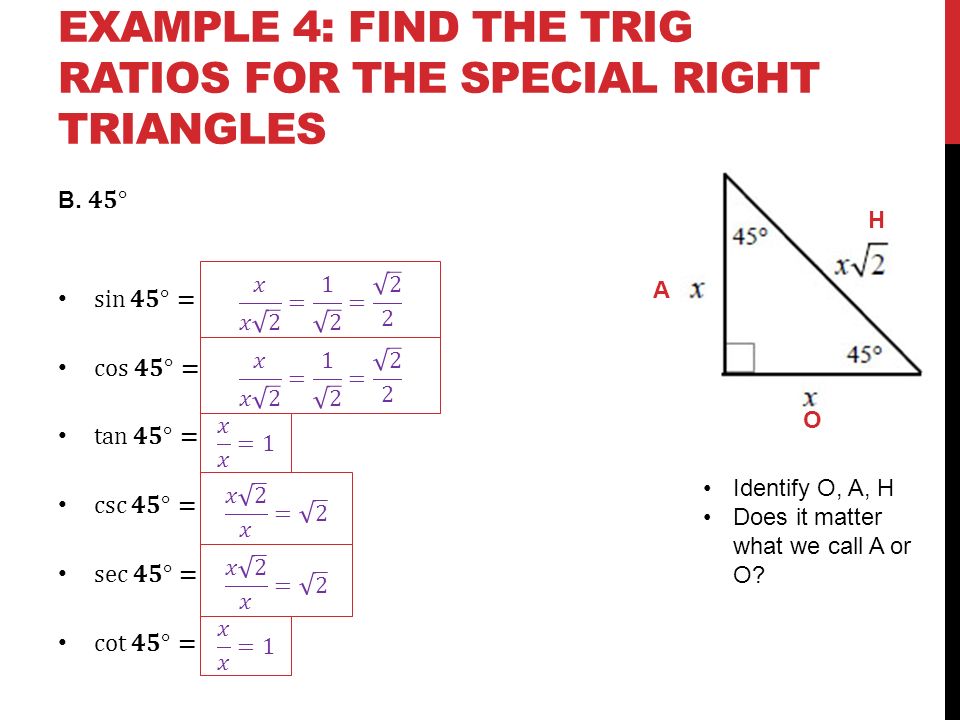
In our special right triangles calculator, we implemented five chosen triangles: two angle-based and three side-based.The purpose of this task is to use the notion of similarity to define the sine and cosine of an acute angle. There are many different rules and choices by which we can choose the triangle and call it special. Their areas are in geometric progression, according to the golden ratio. The sides of the square will be the shorter length in the ratio and the value of x. Right triangle, the sides of which are in a geometric progression (Kepler triangle). The diagonal of the square divides it into two 45-45-90 triangles. These are useful since they allow us to find the values of trigonometric functions of multiples of 30 and 45. However, it is possible to evaluate the trig functions for certain angles without using a calculator. Until now, we have used the calculator to evaluate the sine, cosine, and tangent of an angle. 45 - 45 - 90 Triangles whose sides have the ratio 1:1:2. Learn to find the sine, cosine, and tangent of 45-45-90 triangles and also 30-60-90 triangles. Using the Pythagorean Theorem and the fact that the legs of this right triangle are equal, Example 2: If the diagonal of a square is 6, find the length of each of its sides.
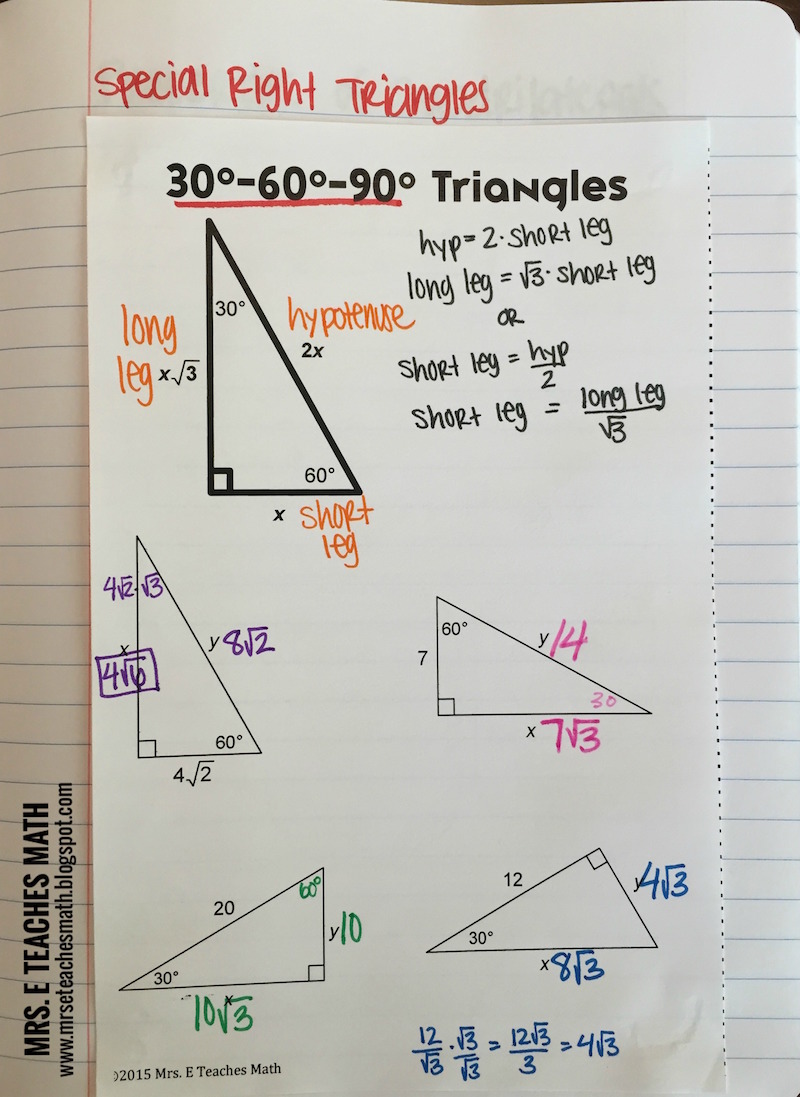
30 - 60 - 90 Triangles whose sides have the ratio 1:3:2. Method 1: Using the ratio x : x : x for isosceles right triangles, then x 3, and the other sides must be 3 and 3. Sides with integer lengths, but almost-isosceles: 20:21:29, 119:120:169, 696:697:985. What are the Special Right Triangles Special Right Triangles.
#SPECIAL RIGHT TRIANGLES RATIOS PLUS#
Of course, the most important special right triangle rule is that they need to have one right angle plus that extra feature.
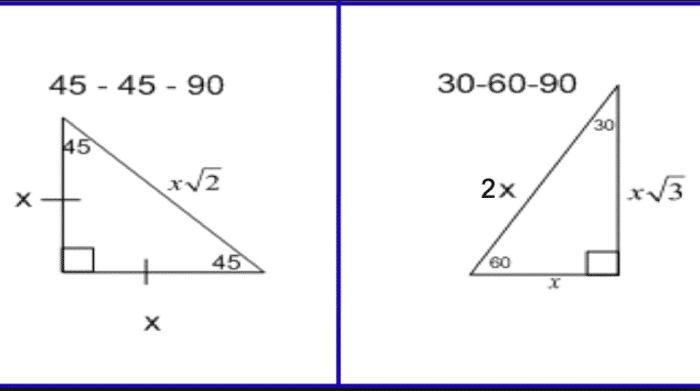
Special right triangles are the triangles that have some specific features which make the calculations easier.


 0 kommentar(er)
0 kommentar(er)
